matematika peminatan kelas X

Fungsi Eksponesial

A. Sifat-sifat Eksponesial

Perhatikan kembali permasalahan perkembangan bakteri di awal bab. Pada awal penelitian tercatat 5 bakteri. Jumlah bakteri akan menjadi dua kali setiap sepuluh menit. Berapakah jumlah bakteri setelah mengalami 1 jam periode perkembangbiakan ? 
\

Contoh Untuk Setiap Sifat

1. 22 x 24 = 22+4 = 26 

2. 22 / 24 = 22-4 = 2-2 
3. (22)4 = 22x8 = 216
4. Lihat jawaban no. 2
    2-2 = 1/22 
5. 23 x 43 = (2 x 4)3 = 83

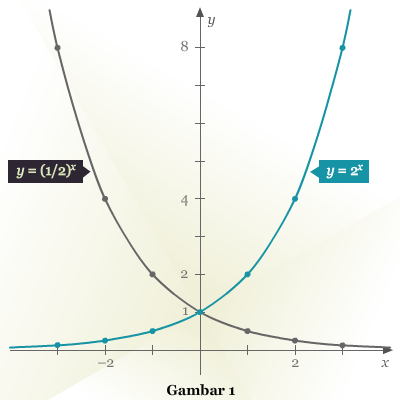
Contoh 2: Grafik Fungsi Eksponensial

Gambarlah grafik masing-masing fungsi berikut.

1. f(x) = 2x
2. g(x) = (1/2)x

Pembahasan Tabel berikut mendaftar x mulai dari –3 sampai 3 dan nilai fungsi-fungsi fdan g yang bersesuaian dengan nilai x tersebut.

Berikut ini grafik dari fungsi-fungsi f dan g pada satu bidang koordinat.

Perhatikan bahwa

sehingga kita dapat menggambar grafik fungsi g dengan mencerminkan grafik fungsi fterhadap sumbu-y.

Gambar 2 menunjukkan grafik dari keluarga fungsi-fungsi eksponensial f(x) = ax untuk beberapa nilai basis a. Semua grafik ini melewati titik (0, 1) karena a0 = 1 untuk a ≠ 0. Kita dapat melihat dari Gambar 2 bahwa terdapat dua jenis fungsi eksponensial: Jika 0 < a < 1, fungsi eksponensial tersebut akan turun. Jika a > 1, fungsi tersebut akan naik.

Sumbu-x merupakan asimtot fungsi eksponensial f(x) = ax. Hal ini dikarenakan jika a > 1, kita mendapatkan ax akan mendekati nol ketika x mendekati –∞, dan jika 0 < a < 1, kita mendapatkan ax akan mendekati 0 ketika x mendekati ∞. Selain itu, ax > 0 untuk setiap xbilangan real, sehingga fungsi f(x) = ax memiliki domain bilangan real dan range (0, ∞).